 This post is a summary of all the polynomial tutorials on this site, put into an annotated order. This is your go-to place for learning about polynomials. If you have a polynomial problem, you’ve come to the right place!
This post is a summary of all the polynomial tutorials on this site, put into an annotated order. This is your go-to place for learning about polynomials. If you have a polynomial problem, you’ve come to the right place!
All Things Polynomial
- To begin, you will need to know the terminology of polynomials. This post helps you to understand ideas such as: degree, term, leading coefficient, constant term, and others. You will also get a brief brush of how to add and subtract polynomials.
- Next, you will want to know how multiply polynomials. The post linked here will tell you two different methods for multiplying: the distributive method (which you may have learned as the FOIL method), and the box method. If you ever get lost keeping track of the terms when you multiply, the box method is a great tool for you to use.
- Now that you can multiply, it’s a good idea to learn how to divide. Here you’ll learn
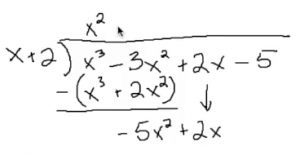 two methods of dividing polynomials. First, polynomial long division, which will work no matter what polynomials you are working with. Second, synthetic division, which only works when you divide by a first degree binomial, like x+2.
two methods of dividing polynomials. First, polynomial long division, which will work no matter what polynomials you are working with. Second, synthetic division, which only works when you divide by a first degree binomial, like x+2. - Sometimes, you will want to know the factors, or roots, of a polynomial. This post addresses how to factor polynomials, with a focus on factoring quadratic equations. Again, There are two methods of factoring presented. I learned the “sit and stare at a pair of parentheses” method when I was in school. Years later a student of mine taught me a pleasantly methodical method – it’s a great tool for factoring trickier quadratics.
- Continuing with quadratics, this post that will explain how to complete the square. Next, another post will help you solve quadratic equations. And then, a post focused on how to graph quadratic functions.
- To factor a polynomial with degree greater than 2, you’ll need to add some tools to your workbench. This post will teach you how to use the rational root theorem to determine factors of a polynomial.
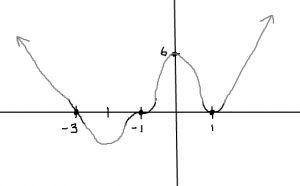
- Once you have a factored polynomial, you’ll want to graph it. Click here to learn how to accurately sketch the end behavior and each interaction with the x-axis.
Et voila!
That’s a whole lot of information about polynomials for you to peruse.
Are there any polynomial-focused topics that I missed? Please let me know with a comment – I’m trying to make this into a thorough resource for math students!
Thanks for sharing this. It has cleared some of my little confusion. So useful post.