Today I’ll explain some of the basics of rational functions. We’ll talk about what rational functions are, how to find their roots, how to find the y-intercept, how to determine the domain, and briefly discuss solving inequalities with rational functions. Before we get started, you should make sure that you’re up-to-speed with polynomial functions; we’ll be using a lot of the same tools that were first explained in those posts.
What’s a Rational Function?
A rational function is any function that is a fraction of two polynomials. You will want to know the degree and leading coefficient of both the numerator and denominator polynomial, and you will want to fully factor both the numerator and denominator if they aren’t factored yet. To start with, let’s play with this rational function:
![]()
The Roots
To find the roots (also known as the zeros, or the x-intercepts), find the x-values that will make the numerator of the rational function equal to zero. In our example:
![]() if
if ![]() or
or ![]() . Therefore the roots are -3 and 2.
. Therefore the roots are -3 and 2.
The y-Intercept
As with any function, you find the y-intercept by plugging in 0 for x and then simplifying the expression. For our rational function:
![]()
Therefore, the y-intercept is at the point ![]() .
.
The Domain
You may recall that the domain of a function tells you all of the x-values that you are allowed to use in the function. Usually, the domain is all real numbers (represented with this symbol: ![]() ), with a few exclusions. The two main things to watch out for when finding out if there are any x’s to exclude are 1. any x-value that will result in dividing by zero, and 2. any x-value that will cause you to take the square root of a negative number. Since rational functions don’t have any square roots in them, we only need to watch out for x’s that will cause the denominator to be 0. In our example:
), with a few exclusions. The two main things to watch out for when finding out if there are any x’s to exclude are 1. any x-value that will result in dividing by zero, and 2. any x-value that will cause you to take the square root of a negative number. Since rational functions don’t have any square roots in them, we only need to watch out for x’s that will cause the denominator to be 0. In our example:
Denominator ![]() , which equals 0 if
, which equals 0 if ![]() or
or ![]() .
.
Therefore our domain is ![]() except when
except when ![]() or
or ![]() .
.
Solving Inequalities
Suppose you are trying to solve a problem where one side of an inequality is a rational function, and the other side is 0.
![]()
Step 1: Write down all of the roots and all of the domain restrictions (I call these the “interesting” x-values). Sort them into increasing order.
Interesting x’s: -3, -1, 2, 4
Step 2: Put those x’s on a number line. They divide the number line into sections. In this case, our four numbers create five sections (less than -3, between -3 and -1, between -1 and 2, between 2 and 4, greater than 4). Put a little 0 above the roots, and a little ![]() above the domain restrictions.
above the domain restrictions.
Step 3: For each section of the number line, plug a value in that section into the original function. Determine if it makes the function positive or negative (you don’t care what the actual value is, just it’s sign). Mark these +’s and -‘s above the number line sections. I call this special number line a Sign Pattern.
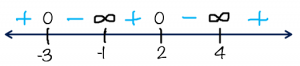
Step 4: If a section has a + above it, then it is a range of numbers where the rational function is greater than 0. If there’s a -, then the function is less than 0. If there’s a 0 above a number, that’s where the function equals 0.
![]() when
when ![]() or
or ![]() or
or ![]() .
.
If we wanted to solve ![]() , look for the negatives and the 0’s:
, look for the negatives and the 0’s:
![]() when
when ![]() or
or ![]()
Looking Forward
Up next will be learning how to use sign patterns to create graphs of rational functions. First we’ll talk about about graphing rational functions using x- and y-intercepts, vertical asymptotes, and horizontal asymptotes using the sign pattern. After that we’ll talk about how to incorporate holes and slant asymptotes into your graphs of rational functions.
Do you have a question? Please ask in the comments!