Today we’re going to begin a dive into trigonometry. Eventually we’ll talk about everything from right triangle trig to the unit circle to trig functions. For now, let’s start at the beginning: Triangle and Trigonometry Basics.
Triangle Basics:
In order to talk about trigonometry, we have to be on the same page about certain facts and standard ways of thinking about triangles. Here are some of them:
Angles
The three angles in a triangle add to 180°. A right angle is a 90° angle, and a right triangle is a triangle containing a right angle. In a right triangle, the two angles that are not the right angle must add to 90°. Those angles are both called acute, meaning that their measure is less than 90°.
Naming Conventions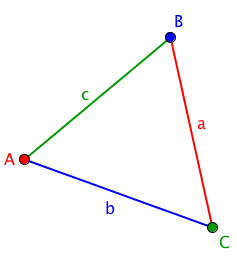
For our purposes, we’ll represent the angles of a triangle with capital letters, usually A, B, and C, and the sides with lower case letters, usually a, b, and c. Angle A is formed by two of the sides of the triangle; side a is “opposite” that angle, or the one side that doesn’t touch angle A. Same with the other sides and angles – if they share a letter, they are opposite each other.
Neat and useful fact: The smallest angle in a triangle is opposite the shortest side. The largest angle is opposite the longest side. And, if you like, the “middlest” angle is opposite the side of middle length.
Finding Right Triangles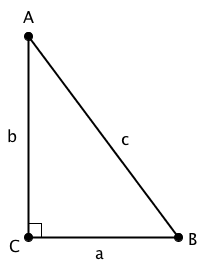
There are a few ways to know that a triangle is a right triangle. First, if you know that a specific angle has a measure of 90°, it’s a right triangle! Sometimes you’ll see a little square drawn into the triangle, as you see at angle C on the right. That little square means that the two lines it touches are perpendicular, another way of telling you that the angle with the little square is a right angle.
Opposite, Adjacent, Hypotenuse
In right triangles, we can use opposite, adjacent, and hypotenuse to talk about the sides of the triangle relative to a particular angle. The names of the sides change if we focus on a different angle. We only use these words when focusing on the acute angles; never the 90° angle.
You already know what I mean if I refer to the side opposite of angle B – it’s the side of a triangle that doesn’t touch angle B. The hypotenuse is the side opposite the right angle. The hypotenuse is the longest side in a right triangle because it’s opposite the biggest angle. The third side, which we haven’t named opposite or hypotenuse, is adjacent to angle B. The adjacent side is the side touching the angle that is not the hypotenuse. In the diagram above, side b is opposite angle B, side c is the hypotenuse, and side a is adjacent to angle B. If we focus on angle A instead of angle B: side a is opposite angle A, aide c is the hypotenuse, and side b is adjacent to angle A.