Tutorial: Un-Multiplying (aka Factoring)

The skill of factoring comes up again and again in math classes. There are easy ways to factor, and hard ways to factor; let’s make sure you know the easy ways!

Basic factoring:

Basic factoring is an investigation into what a collection of terms has in common. If all of the terms in an expression have a thing in common, you can remove that commonality. For example, in the expression $3x^4-12x^3+9x^2$ , each term has a multiple of three and is a multiple of $x^2$ , meaning that 3 and $x^2$ are factors. Now that you’ve figured out the factors you can rewrite the expression as $3x^2(x^2-4x+3)$ . Factoring is rewriting expressions as the product of two (or more) other expressions. Now that we’ve factored out the $3x^2$ , we’re left with a quadratic. Keep reading to learn about factoring quadratic expressions.

Factoring quadratic expressions can be a bit more tricky.

When I learned how to factor quadratics in school, the technique was basically to stare at a pair of parentheses until inspiration struck and the quadratic was factored. For some people, that method is sufficient. For others, inspiration takes its sweet time waiting to strike, especially when the leading coefficient is anything other than 1.

Want some practice?

$x^2-x-6$
$2x^2+5x+3$
$12x^2+x-1$
$6x^2+17x+12$

Success? If not, I’ve got a great step-by-step technique that one of my students showed me.

Methodical Factoring

Think of the quadratic coefficients at 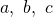$a,\ b,\ c$ : as in 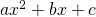$ax^2+bx+c$ . Find the product of $a$ and $c$ (in other words, multiply the leading coefficient by the constant term).
Write down all pairs of numbers that can multiply to $ac$ .
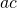If the 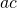$ac$ product is positive, select the pair that adds to 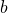$b$ . If the product is negative, pick the pair that has a difference of 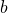$b$ and decide which one to make negative.
Rewrite the original quadratic, except split the 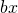$bx$ up into the sum of the two factors.
Factor by grouping, twice, and you’re done!

Now for an example (problem 1 above):

$x^2-x-6$
$a=1,\ b=-1,\ c=-6$ .
$ac = -6$
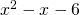
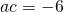
Factors of 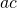$ac$ : 1 & 6, 2 & 3.
Factor pair that has a difference of 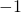$-1$ : 2 & 3. How?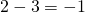 $2 - 3 = -1$
Rewrite middle term: $x^2+2x-3x-6$
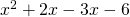
Factor by grouping: $x^2+2x = x(x+2)$ , $-3x-6 = -3(x+2)$ .
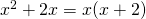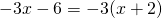Rewrite: 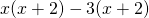$x(x+2)-3(x+2)$ , then factor again: 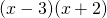$(x-3)(x+2)$ . Factored!!

In Action!

Want to see me use this technique to factor each of the 4 problems? Watch this video. If you just want the answers, check below!

Answers:

$x^2-x-6 = (x-3)(x+2)$
$2x^2+5x+3 = (2x+3)(x+1)$
$12x^2+x-1 = (4x-1)(3x+1)$
$6x^2+17x+12 = (2x+3)(3x+4)$

Did you learn something new? Do you have a question? Is there a particular problem you want to see factored? Please let me know by leaving a comment below!