“Completing the Square” is an algebra skill that you will need to use when you’re playing with quadratics, circles, and (other) conic sections. Once you get the hang of it it’s no big deal, but it can be a bit mystifying until then. Let’s clear it up, and then for a bonus, I’ll show you were the quadratic formula comes from.
First, things we know about squares:
- Geometrically:
- Both sides are the same length
- The area is equal to side length times side length
- Algebraically:
- A perfect square is a number equal to an integer multiplied by itself.
- If an expression is squared, it looks like:
.
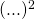Next, make sure you’re familiar with the box method of multiplying polynomials; it will come in handy shortly!
Completing the Square is Solving a Puzzle
Let’s say we have the expression 
and we’re asked to complete the square. Really, you’re being asked to write an equivalent expression that has 
in it.
Start by setting up a square with the box method. We know that the area of the square will represent the product of the side lengths, and the side lengths must be the same (because it’s a square). Using what we know about the box method, we can put the 
term in the top left corner. The terms with 
need to be in the top right and bottom left corners, and they need to add to 
. Because we’re dealing with a square, we want it to be balanced, so we’ll put 
in each of those corners. The total area we’ve filled in is equal to our original expression, . However, the square is not “complete” because there isn’t anything in the lower right corner. Working backwards from the box method, you can figure out that the side lengths must both be 
. Once you fill that in, you can see that you can complete the square by putting 9 into that lower right corner. Adding 9 “completes the square.”
This means that you’ve turned into 
. The square is complete, but you’ve changed the value of the expression by adding 
. To fix it, also subtract : 
. Our sleuthing with the box method told us that is equivalent to 
, so you can substitute that in.
In the end, 
. You’ve completed the square and made sure that the value of the original expression is intact.
Can you complete the square for the expression 
?
What about 
? And 
?
Here’s a video walking you through completing the square for , , , and .
What does the Quadratic Formula have to do with completing the square?
Begin with a generic quadratic equation: 
Divide everything by 
: 
Complete the square: 
Start solving for : 
Simplify left side: 
Take square root of both sides: 
Simplify left denominator: 
Solve for : 
Simplify: 
Hey! I know that formula!
I love seeing different ways to do a Math problem. Your explanation has given me a whole new meaning to ‘completing the square’ – thank you.
I’m so glad you like it! When I learned completing the square it was simply an algebraic algorithm (divide b in half, square it, etc). The visual method helps the algebraic algorithm make so much more intuitive sense for me.